But what if it's just randomness?
I gathered the data on every college football game from this past season, resulting in 872 games (including FCS opponents). I filtered down to only FBS vs FBS, resulting in 774 games.
There were 6,975 scores (defined as a TD, FG, or defensive score, so that extra points don't count twice) in this past season. I removed the 774 that were the first score of the game, leaving me with 6,201 to analyze. I split these between "momentum scores", i.e. scores that followed a score by the same team, and "counter scores", i.e. scores that followed a score by the other team. The initial results seemed pretty damning:
| Total Scores | 6,201 | |
| Momentum Scores | 2,802 | 45.19% |
| Counter Scores | 3,399 | 54.81% |
Not only does momentum not appear to exist, but this seems to show evidence against it! That being said, the opposing offense almost always gets the ball next (barring an onside kick or a turnover on the kick return). This obviously greatly increases the chance of a "counter score" since the other offense has the ball, unless we believe that "momentum" affects both the offense and defense on the same team. The above data seems to strongly counter that hypothesis; testing this against the assumption that "momentum" or "counter" scores occur at a 50/50 rate results in a z-score of -7.62, which translates to a 0.0000000000013% chance that that hypothesis is correct.
So how can we prove whether momentum exists or not? That's a tall task, so my focus is more on showing whether there is an actual trend that occurs, or whether it's likely randomness.
To illustrate this, think about a series of 100 coin flips. You would expect there to be 50 heads and 50 tails (this is the "expected value") at the end, but this isn't always the case due to natural variance (i.e. randomness). Even within this series you will see streaks due to this randomness: if you flip a coin 3 consecutive times, the odds of seeing 3 heads in a row is 1/8, or 12.5%. But overall, there is almost a 99% chance that you will see 3 consecutive heads in those 100 flips.
I took this idea and applied it to streaks of scores, meaning the number of consecutive times one team scored without their opponent scoring. I hypothesized that these streaks would follow the exponential distribution, which has the following density function and graph:

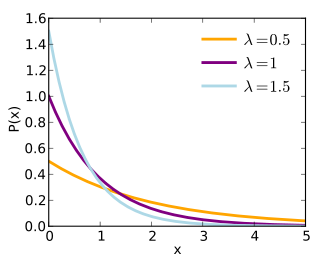
Setting λ = 0.9 results in the following comparison between what actually occurred in the data, Actual f(x), and what the theoretical function returns, Expected f(x):
| Streak | Frequency | Actual | Expected |
| 1 | 3399 | 0.548 | 0.603 |
| 2 | 1556 | 0.251 | 0.245 |
| 3 | 659 | 0.106 | 0.100 |
| 4 | 294 | 0.047 | 0.041 |
| 5 | 142 | 0.023 | 0.016 |
| 6 | 72 | 0.012 | 0.007 |
| 7 | 44 | 0.007 | 0.003 |
| 8 | 22 | 0.004 | 0.001 |
| 9 | 11 | 0.002 | 0.000 |
| 10 | 2 | 0.000 | 0.000 |
Graphing these functions together show that they are almost completely superimposed on one another:
The only "streak" that differs significantly from the theoretical function is a streak of 1, which might be explained by the previously described fact that the opposing team usually gets the ball following their opponent's score. It certainly seems that the exponential distribution fits this data, thus indicating that momentum does not actually exist (in college football), but is rather a construct of trying to explain randomness.
No comments:
Post a Comment