How To Create a Simplex Linear Program Algorithm in Excel (Solver)

Calculating the optimal solution of a simplex linear program algorithm (simplex LP), using matrix math, by hand, is not that easy. But doing so in Excel, using Solver, is!

To illustrate, I'll calculate an optimal fantasy football lineup for this Sunday's Week 13 games. Of course, optimizing a simplex LP is straight-forward as long as the functions are linear - the hard part is devising an accurate projection system to maximize on. 

The Excel is linked here for download. First, you'll need to load the Solver add-in. Then you'll need to identify:

• Objective function (max, min, or equal to a value)
• In this example, maximize projected fantasy points
• Variables
• In this example, binary variables identifying which players to draft
• Constraints
• In this example, a few:
• Salary <= $50,000
• Exact number of players in each position
• All variables are binary

For doing this in Excel, using SUM and SUMPRODUCT are the building blocks to make sure the linearity constraint is satisfied. Additionally, SUMIF is very useful because it only allows for one criteria - while you can still violate linearity depending upon the criteria, SUMIF is easier for troubleshooting which formula broke your code (whereas SUMIFS has an unlimited number of criteria).

Column F contains our variables, column G contains our objective (maximize), and column J contains one of our constraints (maximize up to $50k).

First, we set up the objective cell and first constraint:

• B1: =SUMPRODUCT($F$2:$F$200,$G$2:$G$200)
• B3: =SUMPRODUCT($F$2:$F$200,$J$2:$J$200) 

We limit to row 200 here because the maximum number of variables the standard Solver plug-in can solve over is 200.

Next we have to constrain the positions:

• QB = 1
• RB = 2
• WR = 3
• TE = 1
• FLEX = 1 (can be RB, WR, or TE)
• DS = 1

So we can get the FLEX position, and keep the program linear, by adapting to:

An example formula for cell B7 =SUMIF(I:I,A7,F:F).

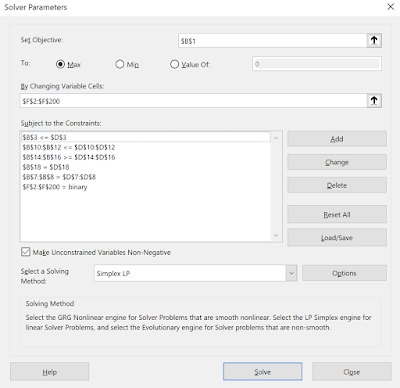
Then we just need to set up Solver, with the added constraint of making $F$2:$F$200 = binary:

This results in a feasible solution, as our problem is set up correctly in a linear fashion:

And results in a lineup projected to score 153.7 points, with a salary of $50,000: