The exponents have been tweaked slightly since James originally derived this formula (I use 1.83 for MLB as opposed to 2), and can also be altered to fit other sports.
So runs scored and runs allowed are used to give a more accurate representation of wins and losses, which can then be used to calculate win percentage. My hypothesis was to take this a level deeper: use hits scored and hits allowed to estimate runs scored and runs allowed to represent wins and losses which then can be used to give win percentage.
Their actual record is 19-26, which gives an actual win percentage of 0.422:
They've scored 179 runs and allowed 201, so their Pythagorean Expectation (Pyth_Runs) estimates their win percentage at 0.447, suggesting they should start winning more games:
Finally, they've scored 382 hits and allowed 392. Multiplying these numbers by the factor of 0.507 estimates their runs scored at 194 and runs allowed at 199, which gives a Pyth_Hits win percentage of 0.488, an even better figure:
| Win %: | 0.422 |
| Pyth_Runs %: | 0.447 |
| Pyth_Hits %: | 0.488 |
However, these results don't mean much in a vacuum. How does each representation of win percentage perform as a way of ranking/rating teams? I tested each of these calculations to predict playoff series results (using regular season data) for the past 5 seasons (for uniformity, I left out the single-elimination wild card games of the past two years).
| Win % | Pyth_Runs | Pyth_Hits | |
| 2009 | 6-1 | 6-1 | 5-2 |
| 2010 | 4-3 | 4-3 | 5-2 |
| 2011 | 3-4 | 3-4 | 4-3 |
| 2012 | 3-4 | 2-5 | 5-2 |
| 2013 | 5-2 | 5-2 | 5-2 |
| Total Correct | 21 | 20 | 23 |
Pyth_Hits had the best record over this 5 year span, and is also the most consistent: Win % and Pyth_Runs have losing records in 2011 and 2012, while Pyth_Hits never does worse than 4-3.
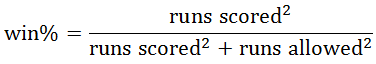



No comments:
Post a Comment