Source: mlb.com
Source: milb.com
As pointed out by my co-worker with the San Jose Giants, inning-by-inning they're identical: each Giants team scored the same runs in the same inning. So just how unlikely is this?
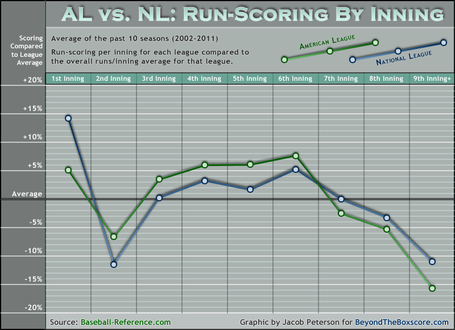
The most likely outcome in any given inning is 0 runs, but even so, the odds of matching inning to inning have to be extremely low, since each half-inning had to have the exact same outcome occur. And, as noted by Beyond the Box Score, the distribution of runs per inning is not uniform:
This makes the math a little bit more tricky, but thanks to Baseball-Reference, all the data needed to calculate this is readily available.
This is what the box score looks like when translated to the percent chance of the number of runs scored in each half of each inning, with the bottom row being the exact probability of that inning occurring:
| Team | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Visitor | 69.53% | 76.72% | 73.69% | 70.42% | 71.49% | 73.75% | 73.79% | 75.57% | 76.25% |
| Giants | 69.53% | 76.72% | 15.20% | 70.42% | 71.49% | 73.75% | 73.79% | 13.85% | 100.00% |
| 48.34% | 58.85% | 11.20% | 49.60% | 51.10% | 54.40% | 54.45% | 10.47% | 76.25% |
Finally, multiplying the bottom row out gives us the probability of that exact box score: 0.0191%. For lack of better data, we'll assume minor leagues roughly follow this same run distribution, meaning the chances of any minor league team and any major league team sharing this same box score are 0.000004%... or 1 in 27,438,500.
But the chances of the minor league team being affiliated with the major league team? The Giants were the major league team, and they have 4 minor league teams. So do the other 29 MLB teams, so there are 120 total minor league teams across Class A, Class A Advanced, Double-A, and Triple-A. 4/120 = 1/30, but since each team has an opponent, there only 15 ongoing games to choose from, so there is a 1/15 chance this exact box score happened with their affiliate: (1/15)*(1/27438500) = 0.00000024%... or 1 in 411,577,489.
And the probability this would occur on the same day? Even more unlikely. Even so, the estimate of 1 in 411,577,489 is a truly remarkable figure.


No comments:
Post a Comment