Le'Veon Bell is currently giving up $853k a week to hold out for a better deal from either the Steelers or another team in free agency next season. That's a lot of money, and with the stalemate growing more contentious and extending past Week 3 at this point, it seems likely he will remain out until Week 11, "when he must report in order to ultimately reach free agency" (per the Washington Post).
Le'Veon Bell is also currently one of the best fantasy football players in the game. He was a consensus top 3 pick until the contract situation really started threatening his likelihood to play, after which he started sliding down draft boards:
With fantasy sports being a $7 billion industry, his holdout on the field is certainly impacting real money off the field. So I was posed this question: is Bell costing his fantasy owners more money than he is himself?
The first step towards answering this is determining how much money is really on the table in traditional fantasy football leagues. I compiled a litany of overall stats on the fantasy industry from the Fantasy Sports Trade Association:
- 59.3 million users play fantasy sports (note that 1 person can play multiple sports)
- 19 million users play fantasy football (32% of all users)
- $184 is the average amount spent annually on "traditional fantasy sports", i.e. non-DFS
- 70% of players pay a league fee
From the above figures I was able to derive a lot, along with some other assumptions. The median football league contains 12 players (the average should be slightly higher due to larger leagues skewing the mean), so I estimate there are about 1.36 million fantasy football leagues out there. Of these, 70% have a league fee, so there are 950k (1.36m * .7) paid leagues.
If the average spend is $184 per player, and 32% of players are playing football, then I'm assuming $59 ($184 * .32) is the average spend on fantasy football leagues. This may seem high since most leagues are a $20 buy-in, but this number will be skewed higher by high rollers playing in leagues that have buy-ins of $1,000+.
This means that the typical league pot is $707 ($59 * 12), resulting in $672.1 million ($707 * 950k paid leagues) being in play across all leagues. But how much is Bell's absence directly costing fantasy players? I'll need to calculate the impact in expected winnings on a team that drafted Bell with a top 3 pick, but has to use a replacement level "third best" RB instead (since 2 running backs start in a typical 12 team PPR league).
First, the expected value of a team in the playoffs: in a 12 team league, I'm assuming 4 teams make the playoffs, and are evenly matched at that point such that each team has a 25% chance to come in 1st/2nd/3rd/4th. A typical payout structure is 60%/30%/10% for 1st/2nd/3rd, so the $707 pot would be split $424/$212/$71. If each spot is equally likely (once you're in the playoffs), the expected value of winnings is $177 ($424 * .25 + $212 * .25 + $71 * .25).
Now I need to simulate the difference between a team without Bell (and a third string replacement) versus an "average" team, and how that affects their chances of making the playoffs.
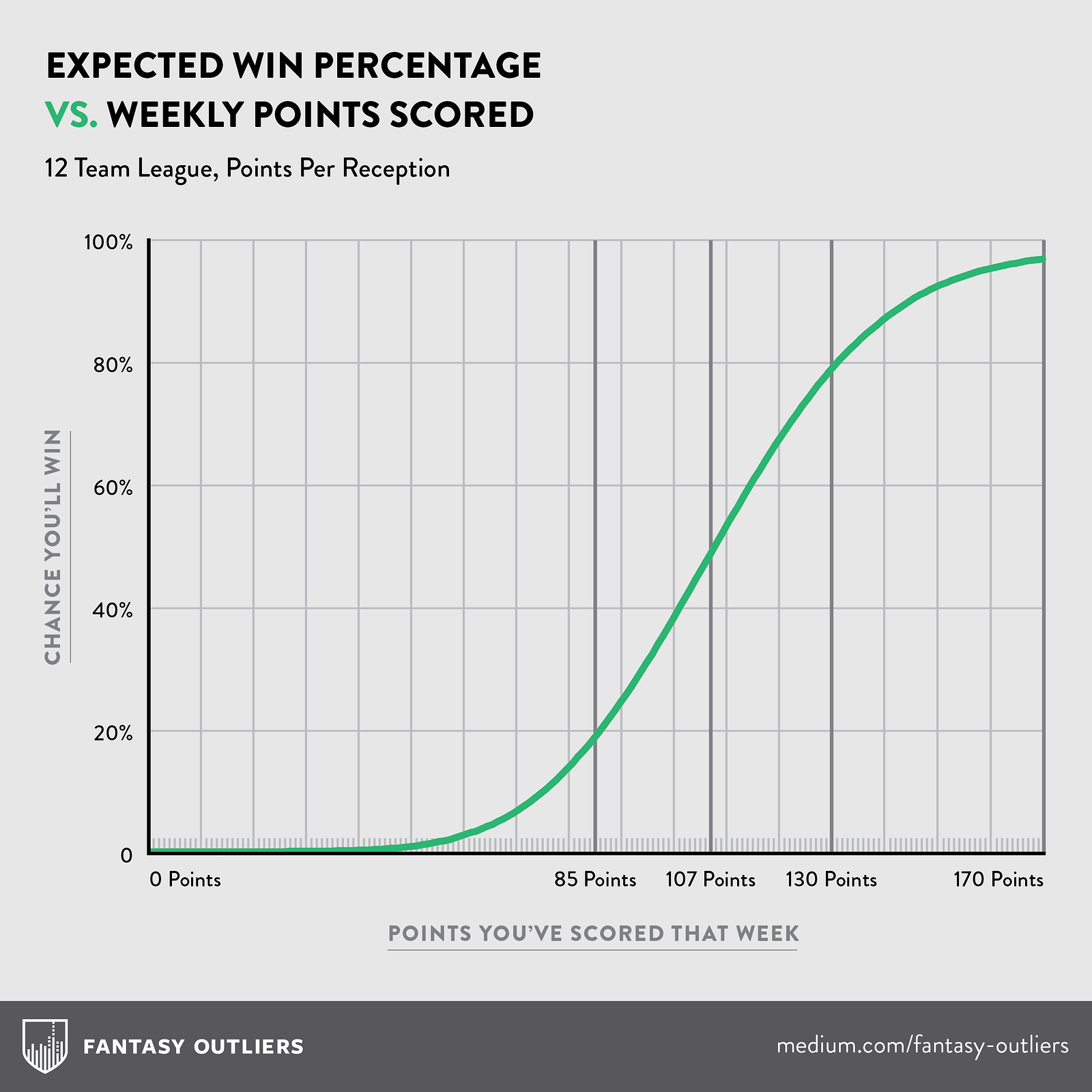
So I simulated two different seasons 10,000 times each: one in which Bell is AWOL for the first 10 weeks of the season, and one in which you (and everyone else) each have an average team all year long. You need at minimum 8 wins to make the playoffs, and you can only expect around 4 without Bell:
In the Bell-less scenario, you would be missing out on 17.3 points for the first 9 weeks of the season, and your chances of making the playoffs are 3.9% per the simulations. Now compare this to an "average" league with your "average" team - you should have a 4/12 chance (33.3%) of making the playoffs, and the simulations more or less back this up, projecting a 31.9% chance your "average" team makes the playoffs.
The final piece here is how much money this drop in playoff odds is costing you. The sum in expected values once in the playoffs is $168 million (950k leagues * $177 expected value in playoffs). Without Bell and a 3.9% chance of making the playoffs, the total expected value is $6.55 million (0.039 * $168 million). With Bell and a 31.9% chance of making the playoffs, the total expected value of an average team is $53.6 million. The difference between those two? $47.05 million, or $4.705 million per week that Bell misses, which completely dwarfs the $853k that Bell is foregoing each week he doesn't play.