Through the first 2 weeks of the NFL season, much has been made of the new rule change that moves the extra point attempt back to the 15-yard line, and for good reason - the success rate on XP is down from 99.3% for all of last season to 94.19% so far this season. The Steelers appear to be going for two more often, but is this 5% decrease in accuracy enough to make the two-point conversion the better strategy?
It comes down to the expected value of each strategy. Over all of last season, teams successfully scored the two-point conversion 47.46% of the time. Thus, the expected value of going for two was 0.949, nearly identical to the current expected value of the extra point, 0.942. However, through a very small sample size of 15, teams have successfully converted for two 53.33% of the time in the first 2 weeks of 2015, which implies an expected value of 1.067. 0.125 points is a large difference, but it remains to be seen if this higher success rate will continue. It's more likely regression to the mean will occur, which leaves the decision between the two options basically a coin flip. It probably will be more dependent on the current game state.
Thursday, September 24, 2015
Wednesday, September 23, 2015
The Most (In)efficient Way to Complete the Taco Bell $20 Challenge
The Taco Bell $20 Challenge is "a game in which a participant or participants must consume twenty US dollars worth of food items from Taco Bell restaurant in one sitting." The goal then should be to get to $20 in the most inefficient way possible: in other words, maximize cost while minimizing the amount of food.
First, a couple of caveats in order to maintain the spirit of the challenge:
I used the weight of each item (in grams) as a proxy for its respective size (since we ultimately care about volume), and then aimed to minimize this within the constraint of spending at least $20. I used a Simplex Linear Program to do so, and found the following optimal order:
Data sources: Prices - Fast Food Menu Prices, Weights - Calorie Count
For contrast, choosing 20 Cinnabon Delights and/or Cinnamon Twists (both are the same price and weight) would be a clearly superior strategy:
But this is banned under my caveat. What if we make things a bit more interesting, and don't allow more than 1 of the same item?
First, a couple of caveats in order to maintain the spirit of the challenge:
- The $20 has to be food only, no drinks
- I removed all dessert items. Otherwise it would be pretty easy: order 20 orders of Cinnamon Twists and/or Cinnabon Delights
I used the weight of each item (in grams) as a proxy for its respective size (since we ultimately care about volume), and then aimed to minimize this within the constraint of spending at least $20. I used a Simplex Linear Program to do so, and found the following optimal order:
Data sources: Prices - Fast Food Menu Prices, Weights - Calorie Count
For contrast, choosing 20 Cinnabon Delights and/or Cinnamon Twists (both are the same price and weight) would be a clearly superior strategy:
But this is banned under my caveat. What if we make things a bit more interesting, and don't allow more than 1 of the same item?
This results in a 19% increase in weight, but adds a bit of variety to the order.
Tuesday, September 15, 2015
"What are the odds?" Down 60 Points, How Likely Was It I Would Come Back in Fantasy Football?
Fantasy football is the greatest/worst, depending upon which side of the final score you're on. In Week 1, I was getting beat down by my opponent, Colin, who had also been talking smack all week. And he had every reason to too: at one point, ESPN's projections had him winning by 60 points. But at the end of the week, this happened:
Just how likely was it I would end up winning the week? Yahoo's fantasy football gives win probabilities in addition to projected points each week. In this upcoming week, I'm favored by 4.75 over my opponent, with a win probability of 55%. By dividing this projected margin of victory by a constant and then treating it as normally distributed, I can estimate the given probability (this is how I make predictions for any given league in real sports). Using the given Yahoo numbers, I estimate that constant to be roughly 35, which now allows me to estimate Colin's win probability given that he was projected to win by 60. And that estimated win probability was 95.68%.
"What are the odds?" The Chances the SJ Giants Come Back to Beat Visalia
Going into the bottom of the 5th inning last night, the San Jose Giants trailed the Visalia Rawhide 4-0, and also were down 2-0 in the best-of-5 series. I was asked "What's the win probability for the game at that point?"
The best way to determine this would be to simulate the rest of the game/series play-by-play, taking into account each player on each team and their respective performance throughout the season. However, I don't quite have my play-by-play simulator ready for baseball (although I'm very close!), so I adapted the simulator I wrote awhile back that simply simulates how many runs are scored in each half-inning. As before, this data was gathered from Baseball-Reference, which shows how frequently 0 runs, 1 run, 2 runs, etc are scored in a half-inning (in MLB in 2015; I'm using this as a proxy for MiLB).
The Giants had to overcome a 4 run deficit in 5 innings. I ran 10,000 simulations, and they only come back to tie the game (or take the lead) by the end of the 9th 2.55% of the time. To ultimately answer the first question, they only win the game 1.78% of the time.
Then there was a followup: "Down 4-0 heading to the bottom of the 5th in a best-of-5 series in which they were down 2 games to none. What was the series win probability at that point?"
We know their odds of winning Game 3 were down to 1.78%, so now we have to determine the odds they subsequently win Game 4 AND 5. Game 4 is at home, while a possible Game 5 would be on the road. Using both teams' second-half records (both finished at .600) in Log5 and factoring in home-field (0.24 runs in MLB) gives San Jose 52.27% to win Game 4 and 47.73% to win Game 5. So the odds of winning both Game 4 and 5 are 24.95%. Finding their series win probability headed into the bottom of the 5th last night is then 1.78% * 24.95% = 0.44%, or about 1 in 225. Even so, that's twice as likely as the Cowboys' comeback over the (New York) Giants on Sunday night.
Given that they did come back and win Game 3 means they're now at 24.95%, or about 1 in 4.
The best way to determine this would be to simulate the rest of the game/series play-by-play, taking into account each player on each team and their respective performance throughout the season. However, I don't quite have my play-by-play simulator ready for baseball (although I'm very close!), so I adapted the simulator I wrote awhile back that simply simulates how many runs are scored in each half-inning. As before, this data was gathered from Baseball-Reference, which shows how frequently 0 runs, 1 run, 2 runs, etc are scored in a half-inning (in MLB in 2015; I'm using this as a proxy for MiLB).
The Giants had to overcome a 4 run deficit in 5 innings. I ran 10,000 simulations, and they only come back to tie the game (or take the lead) by the end of the 9th 2.55% of the time. To ultimately answer the first question, they only win the game 1.78% of the time.
Then there was a followup: "Down 4-0 heading to the bottom of the 5th in a best-of-5 series in which they were down 2 games to none. What was the series win probability at that point?"
We know their odds of winning Game 3 were down to 1.78%, so now we have to determine the odds they subsequently win Game 4 AND 5. Game 4 is at home, while a possible Game 5 would be on the road. Using both teams' second-half records (both finished at .600) in Log5 and factoring in home-field (0.24 runs in MLB) gives San Jose 52.27% to win Game 4 and 47.73% to win Game 5. So the odds of winning both Game 4 and 5 are 24.95%. Finding their series win probability headed into the bottom of the 5th last night is then 1.78% * 24.95% = 0.44%, or about 1 in 225. Even so, that's twice as likely as the Cowboys' comeback over the (New York) Giants on Sunday night.
Given that they did come back and win Game 3 means they're now at 24.95%, or about 1 in 4.
Sunday, September 13, 2015
Is Running the Ball Really "Safer"?
Conventional wisdom dictates that rushing the football is a "safer" option than passing due to a lower risk of a turnover. However, does this increased security justify the decreased expected yardage compared to passing?
To start, I looked at the average yards gained per attempt for rushing vs passing, based on the 2014 NFL season.
Data from Football-Reference
To start, I looked at the average yards gained per attempt for rushing vs passing, based on the 2014 NFL season.
| Type | Rushing | Passing |
| Yards | 57002 | 121247 |
| # Attempts | 13688 | 17879 |
| Yds/Attempt | 4.16 | 6.78 |
Note that this is over all passing attempts, not just completions. Even taking into account incomplete passes (which gain 0 yards) and negative sack yardage (which, in NFL, are deducted from passing yards), passing the ball clearly gives larger expected yardage, by 2.62 yards per play. However, the threat of an interception means rushing is "safer"... right?
Fumbles occurred on 4.89% of rushing attempts, while interceptions occurred on 2.52% of passing attempts. However, the offense can recover a fumble, and does so 37.9% of the time on rushing plays, with the defense recovering the other 62.1%. Factoring this into the above figure means 3.04% of rushing attempts result in a turnover.
| Type | Rushing | Passing |
| Attempts | 13688 | 17879 |
| INT/FUM | 670 | 450 |
| Turnovers | 416 | 450 |
| TO Rate | 3.04% | 2.52% |
So in the end, rushing is MORE risky turnover-wise than passing (or at least it was in the 2014 season).
This doesn't mean teams should pass the ball 100% of the time: there's still game theory to be considered. However, the above results counter conventional wisdom, and imply that teams are both leaving yards on the table AND are risking more turnovers by running the ball too often.
Saturday, September 5, 2015
Going 1st vs Going 2nd in Overtime in NCAAF
The conventional wisdom in college football is that once a game goes to overtime, the ideal strategy is to go second. That way you know exactly what you need to score to extend the game or win it outright, similar to batting in the bottom of the inning in baseball.
I sought to find out if past results support this idea. I looked at every game that went to overtime in the past two seasons, and then took the final overtime period to determine which team went first or second (so in a 3OT game, for example, the team that went second in that third OT was the team that ultimately went second to end the game). Over 67 games, the team that went second won 55.22% of the time. Testing this against the hypothesis of 50% (it doesn't matter whether you go first or second) gave a corresponding p-value of 0.197. This isn't definitive, but this does give some slight evidence that going second is the correct strategy.
I sought to find out if past results support this idea. I looked at every game that went to overtime in the past two seasons, and then took the final overtime period to determine which team went first or second (so in a 3OT game, for example, the team that went second in that third OT was the team that ultimately went second to end the game). Over 67 games, the team that went second won 55.22% of the time. Testing this against the hypothesis of 50% (it doesn't matter whether you go first or second) gave a corresponding p-value of 0.197. This isn't definitive, but this does give some slight evidence that going second is the correct strategy.
Friday, September 4, 2015
I Hate Being a Fan of Carolina Football
I hate being a fan of Carolina football. To paraphrase my uncle, "Carolina football is a tease at best and heartbreak at worst" (that's the PC version). That's the ceiling of the fan experience watching us play: hope with the persistent gut feeling that no matter what, in the end, we're going to blow it.
2008, Meineke Car Care Bowl, West Virginia, semi-home in Charlotte. Back and forth game, but we lead in the fourth. West Virginia goes up by 1 midway through the quarter, but we start driving down the field needing only a field goal. Interception with under 2 minutes to play. L
2009, Meineke Car Care Bowl, Pittsburgh, Charlotte again. Back and forth game, again, but we lead, again, late into the fourth. Pitt kicks the winning field goal with 0:52 remaining. L
2013, Miami, ranked #10, the first/last night game in Kenan Stadium in years. We outplay them the whole game. Have the lead the whole game. Duke Johnson goes out early, injured. Doesn't matter. Miami runs the ball straight down the field to take the lead with little time left. L
2014, Notre Dame, they're emerging as a possible playoff contender, we're riding a 3-game losing streak with nothing to lose. We go up 14-0 early on great defensive plays. Still no chance. L
This pattern of maddening consistent mediocrity is why, regardless of whether we control the game against a good opponent, I still hold the bitter resignation at all times that that "L" is inevitable.
It's why, halfway through the second quarter, when we had the lead and were quite frankly dominating the game, all of my college friends and I were convinced we were going to lose anyway. It's why, once we got the ball inside the 20 on that last drive, having moved it down the field with little resistance thus far, that I texted "time for us to turn it over", and no one disagreed with that statement. Of course, this proved true moments later with a pick in the end zone. So on that note, and the ultimate point of this "analysis": we didn't convert in the red zone. That's why we lost.
The Ol' Ball Coach is right.
The average red zone conversion rate (defined as either successfully scoring a touchdown OR a field goal once inside the 20) in 2014 was 81.78%. We ranked 87th in FBS last year with 79.59% (but had ranked 12th in 2013 with 90.70%). Even that 87th-best success rate would have been good enough last night. Instead, the following happened (and I'm including when we got to the 21 to illustrate my point):
1st Quarter
Ball at the SC 6. Interception in the end zone, 0/1
Ball at the SC 21. Touchdown! 1/2
2nd Quarter
Ball to the SC 15, sacked back to the SC 21 (getting to the 15 makes this a red zone opportunity). Field goal! 2/3
3rd Quarter
Ball to the SC 21. Interception inside the 20. 2/4
4th Quarter
Ball to the SC 8. Interception in the end zone, 2/5
40% success rate. Less than half the national average. If we get anything out of one of those three opportunities, we win that ball game. But of course, we didn't, and we start the season 0-1, having lost a game we definitely should have won.
L
2008, Meineke Car Care Bowl, West Virginia, semi-home in Charlotte. Back and forth game, but we lead in the fourth. West Virginia goes up by 1 midway through the quarter, but we start driving down the field needing only a field goal. Interception with under 2 minutes to play. L
2009, Meineke Car Care Bowl, Pittsburgh, Charlotte again. Back and forth game, again, but we lead, again, late into the fourth. Pitt kicks the winning field goal with 0:52 remaining. L
2013, Miami, ranked #10, the first/last night game in Kenan Stadium in years. We outplay them the whole game. Have the lead the whole game. Duke Johnson goes out early, injured. Doesn't matter. Miami runs the ball straight down the field to take the lead with little time left. L
2014, Notre Dame, they're emerging as a possible playoff contender, we're riding a 3-game losing streak with nothing to lose. We go up 14-0 early on great defensive plays. Still no chance. L
This pattern of maddening consistent mediocrity is why, regardless of whether we control the game against a good opponent, I still hold the bitter resignation at all times that that "L" is inevitable.
It's why, halfway through the second quarter, when we had the lead and were quite frankly dominating the game, all of my college friends and I were convinced we were going to lose anyway. It's why, once we got the ball inside the 20 on that last drive, having moved it down the field with little resistance thus far, that I texted "time for us to turn it over", and no one disagreed with that statement. Of course, this proved true moments later with a pick in the end zone. So on that note, and the ultimate point of this "analysis": we didn't convert in the red zone. That's why we lost.
Spurrier: How many yards they have?
"440"
Spurrier: Yeah, 440 and 13 points. That don't match up
— Chip Patterson (@Chip_Patterson) September 4, 2015
The Ol' Ball Coach is right.
The average red zone conversion rate (defined as either successfully scoring a touchdown OR a field goal once inside the 20) in 2014 was 81.78%. We ranked 87th in FBS last year with 79.59% (but had ranked 12th in 2013 with 90.70%). Even that 87th-best success rate would have been good enough last night. Instead, the following happened (and I'm including when we got to the 21 to illustrate my point):
1st Quarter
Ball at the SC 6. Interception in the end zone, 0/1
Ball at the SC 21. Touchdown! 1/2
2nd Quarter
Ball to the SC 15, sacked back to the SC 21 (getting to the 15 makes this a red zone opportunity). Field goal! 2/3
3rd Quarter
Ball to the SC 21. Interception inside the 20. 2/4
4th Quarter
Ball to the SC 8. Interception in the end zone, 2/5
40% success rate. Less than half the national average. If we get anything out of one of those three opportunities, we win that ball game. But of course, we didn't, and we start the season 0-1, having lost a game we definitely should have won.
L
Thursday, September 3, 2015
Whether Kick Returners Should Return Kickoffs Out of the End Zone (NCAAF)
College football literally kicks off today, and so this topic seemed like a good fit. As a college football fan, few moments are as frustrating as when a kick returner receives the kickoff in his own end zone and then proceeds to try to take it out and go for the big return. With the recent rule change, taking a knee gets you 25 free yards! So I sought to see whether reality backs my suspicion that, in general, attempting to return the kickoff out of the end zone is not an optimal strategy.
I took a clustered simple random sample of 75 games from the 2014 season (resulting in 797 data points of kickoffs (an average of 10.63 per game)), and then broke things down by looking at only the "eligible" kickoffs (those that went into the end zone, i.e. 65 yards (unless a penalty moved the kickoff up or back)). Unfortunately, stats aren't kept in college football to show how deep into the end zone the kick went, so all I know is whether it broke the plane of the goal line.
69.54% of the time the returner took the touchback, resulting in an automatic 25 yards. Of that other 30.46%, the average return was 23.85 yards (I disregarded returns that had penalties on the returning team). ~24 yards a return is actually much closer to the 25 break-even point than I expected.
But what if you take into account the possibility of a momentum-changing 100-yard return for a touchdown? This occurred only 2.07% of the time, thus implying that your expected value from the return (out of the end zone) alone is 0.14 points. However, 1.38% of the time the returner fumbled and turned the ball over, which is a momentum-changing swing in the other direction. Turning the ball over deep in your own territory leads to a very high probability of giving up at least a field goal, and in my sample, 60% of turnovers resulted in a FG, while the other 40% resulted in a TD. Thus, your expected value in these instances is -0.06, which gives a net expected value from touchdowns/turnovers of 0.08.
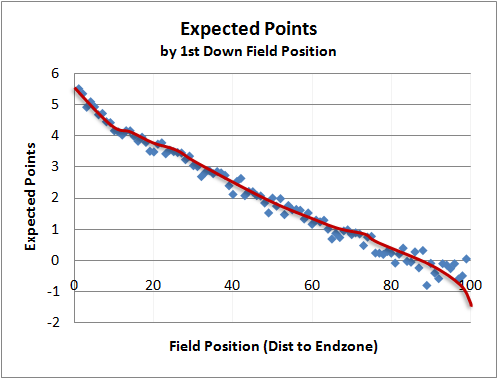
So does this net expected value of 0.08 make up for the 1.15-yard gap between the average return and the 25-yard touchback? This post (for NFL, but I'm using it as an approximate for NCAAF) shows that the expected points from 1st and 10 at the 25 yard line (75 yards from the end zone) appears to be about 0.2:
I took a clustered simple random sample of 75 games from the 2014 season (resulting in 797 data points of kickoffs (an average of 10.63 per game)), and then broke things down by looking at only the "eligible" kickoffs (those that went into the end zone, i.e. 65 yards (unless a penalty moved the kickoff up or back)). Unfortunately, stats aren't kept in college football to show how deep into the end zone the kick went, so all I know is whether it broke the plane of the goal line.
69.54% of the time the returner took the touchback, resulting in an automatic 25 yards. Of that other 30.46%, the average return was 23.85 yards (I disregarded returns that had penalties on the returning team). ~24 yards a return is actually much closer to the 25 break-even point than I expected.
But what if you take into account the possibility of a momentum-changing 100-yard return for a touchdown? This occurred only 2.07% of the time, thus implying that your expected value from the return (out of the end zone) alone is 0.14 points. However, 1.38% of the time the returner fumbled and turned the ball over, which is a momentum-changing swing in the other direction. Turning the ball over deep in your own territory leads to a very high probability of giving up at least a field goal, and in my sample, 60% of turnovers resulted in a FG, while the other 40% resulted in a TD. Thus, your expected value in these instances is -0.06, which gives a net expected value from touchdowns/turnovers of 0.08.
So does this net expected value of 0.08 make up for the 1.15-yard gap between the average return and the 25-yard touchback? This post (for NFL, but I'm using it as an approximate for NCAAF) shows that the expected points from 1st and 10 at the 25 yard line (75 yards from the end zone) appears to be about 0.2:
But the difference between the 24-yardline and the 25-yardline? Roughly 0.1, which is right on par with the 0.08 net expected value. Thus I have to ultimately conclude that the expected payoff of returning the ball out of the end zone is about the same as conservatively taking the 25-yard touchback. This doesn't mean I still won't jump out of my chair and yell at the TV when the returner does it though.
Subscribe to:
Posts (Atom)